PhD's web site

Maple package dcfun

Publications

MathExp Team

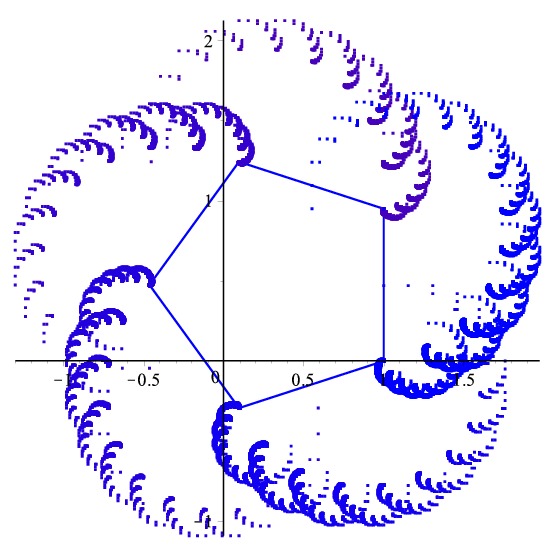
With \(\vartheta = 2\pi/5\), define two matrices $$ A_0 = \left(\begin{array}{cc} \cos\vartheta & 0 \\ 0 & \cos\vartheta \end{array}\right), \qquad A_1 = \left(\begin{array}{cc} 0 & -\sin\vartheta \\ \sin\vartheta & 0 \end{array}\right), $$ and an initial vector $$v_0 = \left(\begin{array}{cc} 1 & 0\end{array}\right)^T.$$ Next consider the sequence \((v_n)\) defined by \(v_0\) and the iteration $$v_{2n} = A_0v_n,\qquad v_{2n+1} = A_1v_n\qquad\text{for \(n\geq 0\).}$$ The picture shows the values of the vector sequence \(s_N\) for \(2^{11} \leq N < 2^{15}\) where \(s_N\) is defined as the summatory function $$s_N = \sum_{n=0}^N v_n,\qquad N\geq 0.$$

It can be shown (See here.) that the sequence \(s_N\) has the following expansion \[ s_N\mathop{=}_{N\rightarrow +\infty} \left(\begin{array}{cc} \cos(\vartheta \log_2 N) & -\sin(\vartheta \log_2 N) \\ \sin(\vartheta \log_2 N) & \cos(\vartheta \log_2 N) \end{array}\right) \Phi(\log_2 N) + O(N^{-0.07}), \] where \(\Phi(t)\) is a \(1\)-periodic vector function. This explains why, when \(N\) is doubled, the drawing is rotated by a fifth of a turn.